
European Space Agency¶

Royal Belgian Institute for Aeronomy¶

G.08 - How is a drift shell defined ?¶
Answer¶
A text extracted from Lemaire et al. (1995, p. 48-51) is reproduced below. The text summarizes the definitions of the different geomagnetic coordinates and clearly explains the concept of magnetic drift shell. The text is part of the TREND-2 final report.
McIlwain’s (1961) L-parameter is defined in terms of the integral I:
\(I=\int_{A}^{A'} \sqrt{1-\frac{B(s)}{B_m}}ds\)
where A and A’ represent the locations of two magnetically conjugate points, and B(s) and ds are the magnetic field intensity and the line element along the field line. A corresponds to the point for which the value of L is sought. \(B_m\) is the magnetic field intensity at the points A and A’. Due to the conservation of the first adiabatic invariant \(\mu\) and of the particle energy E, \(B_m\) is an adiabatic invariant of motion for all particles mirroring at A and A’. Due to the conservation of the second invariant of motion J, I also is an adiabatic invariant for all particles mirroring at A and A’.
These properties have led to the introduction of the (\(B_m\), I) coordinates to map perpendicular integral fluxes J and differential fluxes j of energetic particles mirroring at A, i.e. with velocities perpendicular to the magnetic field vector B and thus with pitch angles \(\alpha = 90\)°. The coordinate pair (\(B_m\), I) uniquely defines the drift shell of all particles mirroring at A. A drift shell is the surface formed by the segments of the magnetic field lines bounded by the intersections of the surfaces B = \(B_m\) and I = cst. It is important to realise that drift shells do not correspond to magnetic shells which are surfaces formed by the magnetic field lines with \(B_{eq}\) = cst (\(B_{eq}\) is the magnetic field intensity on the magnetic equator) and extend down to the surface of the Earth (see Figure 1 below).
In a pure dipole magnetic field, the magnetic field distribution is axisymmetric with respect to the magnetic axis, and thus drift shells are axisymmetric as well. On the basis of this property, McIlwain (1961) found it more convenient and appealing to introduce a more geometrically meaningful parameter \(L_m\), which corresponds to the equatorial radius of a drift shell in the case of a dipole field. McIlwain extended this definition to non-dipole field distributions, such as the geomagnetic field, by applying the functional relation between \(L_m\), \(B_m\), and I, derived for a dipole field, to non-dipole field distributions. \(L_m\) is unambiguously determined for each point on a closed magnetic field line, using (\(B_m\), I) computed with a model magnetic field distribution (including external field models). Consequently, the coordinate pair (\(B_m\), \(L_m\)) is equivalent to the coordinate pair (\(B_m\), I). Usually, the index m is dropped and the McIlwain coordinates are denoted by (B, L).
For particles with pitch angles alpha not equal to 90°, A and A’ are not mirror points. Consequently, neither B, nor I, nor L then are invariants of motion, and, although it has become common usage, it is not appropriate to map J or j, measured by a directional detector, in (B, L) coordinates.
The mirror point M of a particle with pitch angle \(\alpha\) not equal to 90°, measured at A, does not coincide with A. The magnetic field intensity \(B_m\) at M is given by
\(B_m = \frac{B}{sin^2 \alpha}\)
The adiabatic invariant I is then obtained by substituting A and A’ by M and M’ in the first equation. \(L_m\) is obtained from (\(B_m\), I) using McIlwain’s (1961) or Hilton’s (1971) algorithm. The coordinates (\(B_m\), \(L_m\)) calculated in this way label the drift shell of particles measured at A with pitch angle \(\alpha\). […]
Particles measured at A with different pitch angles will move on different drift shells, which are uniquely defined by (\(B_m\), \(L_m\)) (see Figure 2 below). This phenomenon is usually called - erroneously - drift shell splitting. This term is misleading since it suggests that a particle is forced onto different drift shells during its longitudinal drift motion, which is not the case. In fact, a given particle always remains on the same drift shell (which is not the same as a magnetic shell!), for any magnetic field configuration in which adiabatic conditions are maintained. Magnetic shells may split, but not drift shells. The dependence on longitude of the radial extent of a drift shell in a non-dipole field causes the well-established effect that a particle’s equatorial radial distance changes with local time. Therefore, as was emphasized by McIlwain (1966), \(L_m\) should not be identified with a fixed distance, but should merely be considered as a label to identify drift shells. Since \(L_m\) is not constant along a field line in a non-dipole magnetic field, it is incorrect to label magnetic field lines with McIlwain’s \(L_m\). The proper way to identify a field line is with (\(B_{eq}\), \(\phi_{eq}\)), where \(\phi_{eq}\) is the longitude of the point where the field line intersects the magnetic equator.
Instead of (\(B_m\), \(L_m\)), the coordinate pair (\(\alpha_0\), \(L_m\)) may be used, where \(\alpha_0\) is the equatorial pitch angle determined as
\(sin^2\alpha_0 = sin^2\alpha \frac{B_0}{B} = \frac{B_0}{B_m}\)
where \(B_0\) is defined as \(B_0 = 0.311653 L_m^{-3}\) and 0.311653 is the value of the geomagnetic moment implemented in McIlwain’s software. This expression for \(B_0\) was used in the building of NASA’s trapped radiation models (Sawyer and Vette 1976, p.8; Singley and Vette 1972, p. 10).
References¶
Hess, W.N., The Radiation Belt and Magnetosphere, Blaisdell Publishing Company (1968)
Hilton, H.H., L Parameter, A New Approximation, J.Geophys.Res. 76 (1971) 6952-6954
Lemaire, J., Johnstone, A.D., Heynderickx, D., Rodgers, D.J., Szita, S. and Pierrard, V., Trapped Radiation Environment Model Development, Aeronomica Acta 393 (1995) 48-51
McIlwain, C.E., Coordinates for Mapping the Distribution of Magnetically Trapped Particles, J.Geophys.Res. 66 (1961) 3681-3691
McIlwain, C.E., Magnetic Coordinates, Space Science Reviews 5 (1966) 585-598
Roederer, J.G., Dynamics of Geomagnetically Trapped Radiation, Springer-Verlag (1970)
Sawyer, D.M. and Vette, J.I., AP-8 Trapped Proton Environment for Solar Maximum and Solar Minimum, NSSDC/WDC-A-R&S 76-06 (1976)
Singley, G.W. and Vette, J.I., A Model Environment for Outer Zone Electrons, NSSDC 72-13 (1972)
Illustration¶
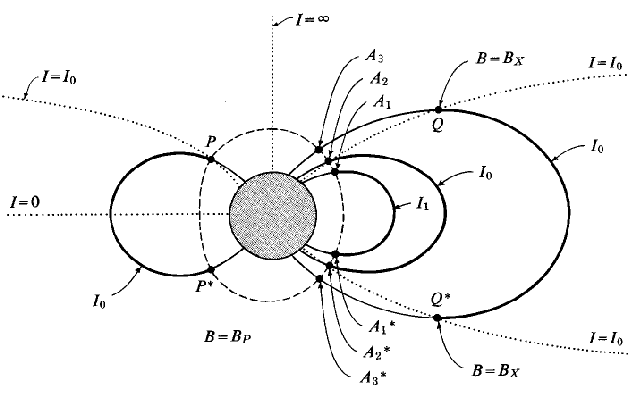
Figure 1: Projection of surfaces of constant \(B_m\) and of constant I. Contours of constant \(B_m\) and of constant I are represented by dashed and dotted lines, respectively. The thick solid lines are the projections of drift shells. Magnetic shells are defined by extension along the magnetic field line to the surface of the Earth, as indicated by the thin solid lines. [Taken from Hess (1968)].
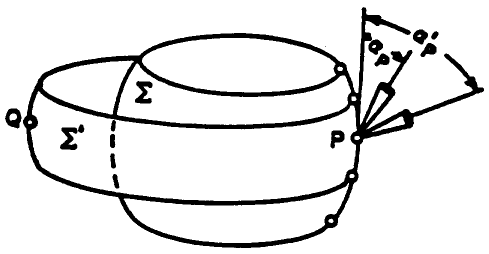
Figure 2: Illustration of the different drift shells for two particles measured at the same point with different pitch angles [from Roederer (1970)].
See also¶
UNILIB/tags/v3.02
